P2850R0
Minimal Compiler Preserved Dependencies

1. Thanks

Our thanks go to the many people who have contributed to this discussion over many years. Hans Boehm, Soham Chakraborty, David Goldblatt, Chung-Kil Hur, Alan Jeffrey, Ori Lahav, Paul McKenney, Scott Owens, Anouk Paradis, Marco Paviotti, William Pugh, James Riely, Jaroslav Ševčík, Ben Simner, Viktor Vafeiadis, Daniel Wright, and others!

2. Introduction

This paper is a step in integrating semantic dependency (sdep) into the C++ standard in order to fix the longstanding thin-air problem. It explains sdep with examples and then poses questions to SG1 members on the finer details of C++ compiler behaviour.

sdep is intended to capture a minimum set of ordering implicit in the data, control and address dependencies of a program -- sdep is made up of only the dependencies that must be preserved by an optimising C++ compiler. [P1780] (Kona 2022) provided standards text introducing sdep as an implementation-defined relation, restricted by a technical report, auxilliary to the standard. Adding sdep is a small change to the standard that fixes a deep problem, avoiding a rewrite of the concurrency specification. We hope this paper will lead to the auxilliary technical report by defining cases where there must be sdep, and the compiler may not optimse, and cases where the compiler must be free to optimise, so there can be no sdep.

We use small example programs with defined outcomes called litmus tests to introduce sdep, and then to discuss the corner cases where the C++ standard should limit the compiler’s optimiser to preseve program order. By convention, locations in litmus tests are atomic and memory accesses are memory_order_relaxed unless otherwise stated.

Target architectures like ARM and POWER allow relaxed concurrent behaviours, that cannot be explained by any sequential scheduling of the memory events in the program. The following litmus test, called Load Buffering (LB), can produce the outcome r1 == 1 && r2 == 1 when translated directly to POWER and ARM targets, so C++ relaxed atomics must be allowed to witness this same behaviour. Similarly, optimisers can reorder events, permitting this behavior even on targets whose architectures forbid the relaxed behaviour.

2.1. Load buffering

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
y := 1

// Thread 1:
r2 := y;
x := 1

The concurrent behaviour of a program is defined by the C++ memory model as a set of executions -- graphs of the memory events performed in one path of the program’s control flow. The memory reads, writes and fences make up the nodes, the black edges represent sequenced before, sb, and the red edges represent reads from, rf, indicating which write each read is reading from. The memory model forbids executions that have the wrong kind of cycles in these relations, but because we must allow the relaxed outcome in the LB test, it cannot forbid executions containing a cycle in sb and rf as below.

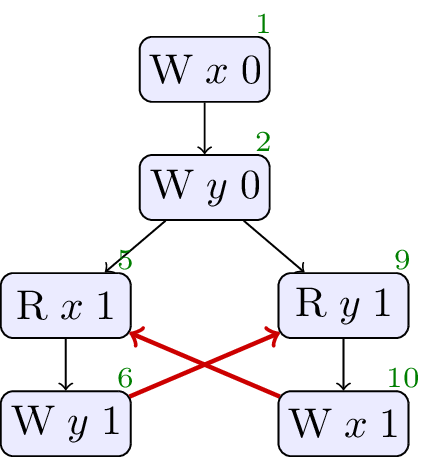
There is a flaw in the existing C++ standard where, in an attempt to allow aggressive compiler optimisation, the language definition goes too far, allowing programs to produce values out of thin air. The test below, LB+datas, is a variant of LB where the values written are taken from the values read on each thread.

2.2. Load buffering with data dependencies

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
y := r1

// Thread 1:
r2 := y;
x := r2

The standard allows the outcomes r1 == 1 && r2 == 1 or even r1 == 42 && r2 == 42 despite the only writes in the program being of value 0: the values 1 and 42 come out of thin air. This is a problem: no combination of compiler optimisations and quirks of the target architecture admits this behaviour, and allowing it is known to make it impossible to prove C++ code correct -- the standard must be changed to forbid this outcome [Problem].

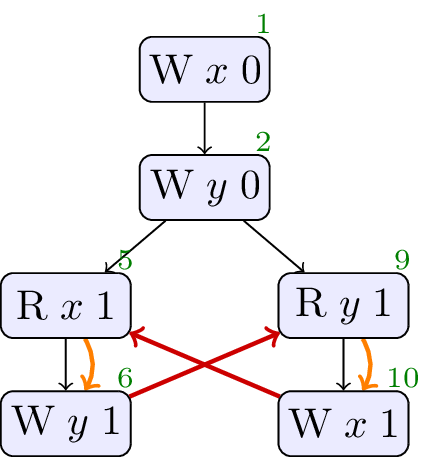
The curved arrows in the executions are dependency edges they reflect the fact that the values written by the writes are data dependent on the values read. In the previous test, LB, there were no dependency edges because concrete values were written making the writes independent. By forbidding cycles in dependency and rf, we could forbid the relaxed outcome here, but keep the outcome in the LB test, just as we need to. Note that this choice restricts the compiler: the specification requires the compiler to keep the accesses in order in LB+datas. That is not an onerous resrtiction: we do not expect the compiler to optimise here.

The next test demonstrates that conditional statements can create dependencies too.

2.3. Load buffering with control dependency

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
if(r1 == 1) {
  y := r1
}

// Thread 1:
r2 := y;
if(r2 == 1) {
  x := 1
}

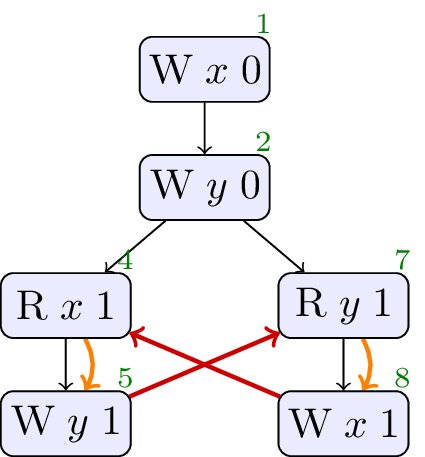
Once again, the execution where r1 == 1 && r2 == 1 is allowed by the current standard, but it should not be. Again, it can be ruled out by forbidding cycles in dependency and rf.

It is not enough to consider only the syntactic structure of the program when calculating dependencies. In the following test, a value loaded from memory is used in a conditional, but because a write of value 1 to x occurs regardless, the compiler may optimise this conditional away.

2.4. Load buffering with false-dependency

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
if(r1 == 1) {
  y := r1
}

// Thread 1:
r2 := y;
if(r2 == 1) {
  x := 1
}
else
{
  x := 1
}

The standard must allow the optimisation. Syntactic dependency, sdep, is a relation that captures just the dependencies that should not be optimised away. In particular, there is no sdep from the load of y to the store of x in this example. There is no cycle in sdep and rf, so the following execution is allowed, as required. In all execution graphs the orange arrows represent sdep.

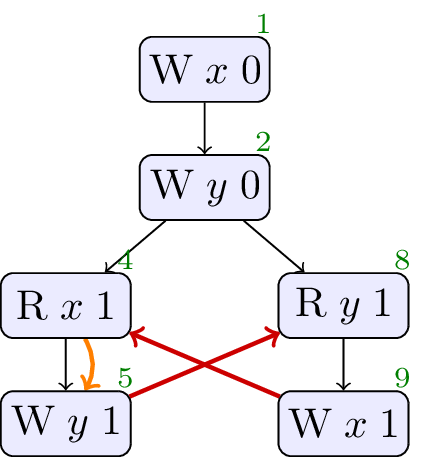
2.5. Java Hotspot

While the audience for this paper is SG1, it is useful to consider other programming languages that have grappled with similar problems. Java has a complex memory consistency model, and they too have had to consider what the meaning of dependency is in their programming language. The following program [Sevcik] is an example where the Java concurrency specification fails to allow all of Hotspot’s optimisations.

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
y := r1

// Thread 1:
r2 := y;
if(r2 == 1) {
  r3 := y;
  x := r3
}
else
{
  x := 1
}

Hotspot will optimise Thread 1 as follows: the load of y in the true branch can take its value from the prior load of y; in the true branch, that load must be of value 1; the true branch now performs a concrete write of 1 to x, just as the false branch does, so there is no need for the conditional; Thread 1 simply loads y into r2 and r3 and writes 1 to x. Now the optimised program can produce the outcome r1 == 1 && r2 == 1 on architectures that exhibit relaxed behaviour in the LB test.

Rather than describe the list of optisations that is performed, sdep is more abstract, describing the dependencies left in each excecution after optimisation. The optimisations described above impact the execution below, where both loads of y on Thread 1 read from the write of value 1 on Thread 0. There is no semantic dependency from the load of x to the write of y because the series of optimisations performed by Hotspot can remove it. The exectuion with outcome r1 == 1 && r2 == 1 is then allowed because there is no cycle in sdep and rf.

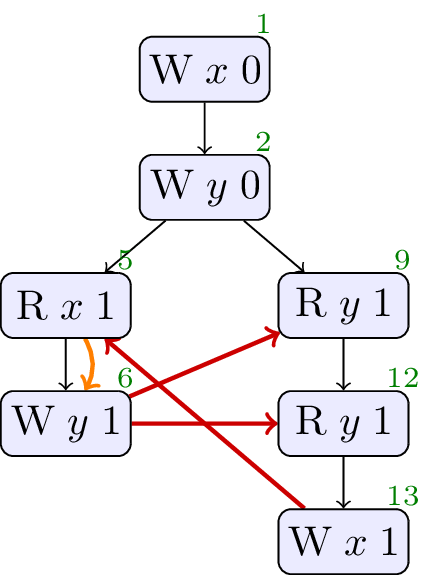
2.6. Java Causality Test Case 18

There is an established set of litmus tests for Java that analyses the effects of dependencies on the memory consistency model, called the Java Causality Tests. Test case 18 highlights the impact of global value-range analysis.

// Init:
x := 0;
y := 0;

// Thread 0:
r3 := x;
if(r3 == 0) {
  x := 42
};
r1 := x;
y := r1

// Thread 1:
r2 := y;
x := r2

A global analysis could determine that the only writes to x in this program are of values 0 and 42. Then on Thread 0, either the inital load of x sees value 42, or the conditional write of x sets it to 42, and in any case, the value of r1 is the concrete value 42. Global value range analysis causes the compiler break the sdep between the loads of x and the store of y.

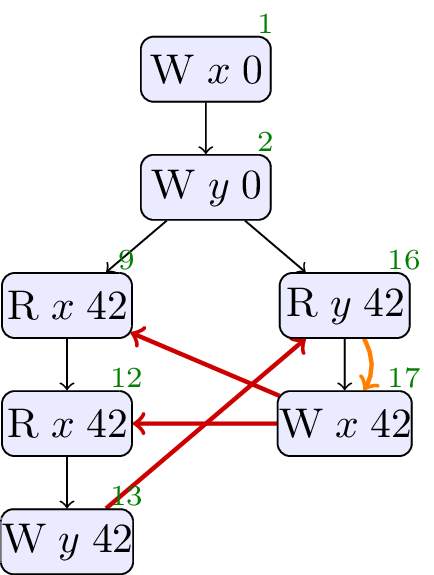
In the execution above, the absence of sdep on Thread 0 means that there is no cycle in sdep and rf, and the outcome where r1 == 42 && r2 == 42 is allowed.

We believe this optimisation should be allowed. Does SG1 agree?

These introductory tests show examples where sdep should, and should not, be present, and higlight the existence of cases where we need to ask to be sure. There are a selection of tests where this choice is less clear-cut and we are interested in SG1’s opinion, we will discuss these next.

3. Controversial Tests

3.1. Goldblatt alignment

First, we will look at an example from previous discussions with SG1 committee members when looking at [P1780]. David Goldblatt pointed out that the compiler may enforce additional constraints on the values used in a program, e.g. aligning objects, and then optimisation may take advantage of these constraints, as in the follwoing example.

struct S {
  float vectorData[8];
};

S s0;
S s1;
S s2;

atomic<S*> x{&s0};
atomic<S*> y{&s1};

S* r1;
S* r2;

void t1() {
  r1 = x.load(rlx);
  if ((uintptr_t)r1 % 32 == 0) {
    y.store(&s2);
  }
}

void t2() {
  r2 = y.load(rlx);
  if ((uintptr_t)r2 % 32 == 0) {
    x.store(&s2);
  }
}

Here t1 and t2 are to be run concurrently. The compiler may have chosen to align all S objects to 32 bytes. With this constraint, the compiler can remove the conditions in t1 and t2: pointers to S-objects will always be mod 32. Therefore, there must not be sdep edges from the loads to the stores in t1 and t2. If this optimisation is allowed, the behaviour allowed by the definition of concurrency is necessarily implementation defined.

We believe compilers do create constraints on values like this, and then optimise in the context of these choices, so there can be no sdep. Does the committee agree?

3.2. RFUB

Continuing with examples from SG1 members, in [P1217R1] Hans Boehm has discussed programs that appear to read from untaken branches.

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
y := r1

// Thread 1:
z := 0;
r2 := y;
if(¬r2 == 42) {
  z := 1;
  r2 := 42
};
x := r2;
r3 := z

In this program, for similar reasons to the Java Hotspot example, a compiler could reason that, no matter what, x is assigned 42 at the end of Thread 1: if Thread 1 did not read 42 from y into r2, then in the conditional, it will set r2 to 42. Optimisation would not remove the conditional entirely: the write of 1 to z is still dependent on the value read from y. Removing the dependency on x yields executions where we observe a store of 42 to x, but not the store of 1 to z.

Does allowing this execution, and chosing this set of sdep edges, match the intention of SG1?

3.3. OOTA4

This example has an execution that is contentious among concurrent models of dependency [PwT]. The program has apparent data dependencies from y to x on Thread 0 and from x to y on Thread 2.

// Init:
x := 0;
y := 0;
z := 0;
b := 0;

// Thread 0:
r2 := y;
r3 := b;
if(¬r3 == 0) {
  x := r2;
  z := r2
}
else
{
  x := 1
}

// Thread 1:
b := 1

// Thread 2:
r1 := x;
y := r1

In the following execution, the rf edges over x and y form a cycle if data dependencies are recognised as sdep edges. In this execution, b reads from the write on Thread 1. We believe that these sdep edges are correct and the execution should be forbidden.

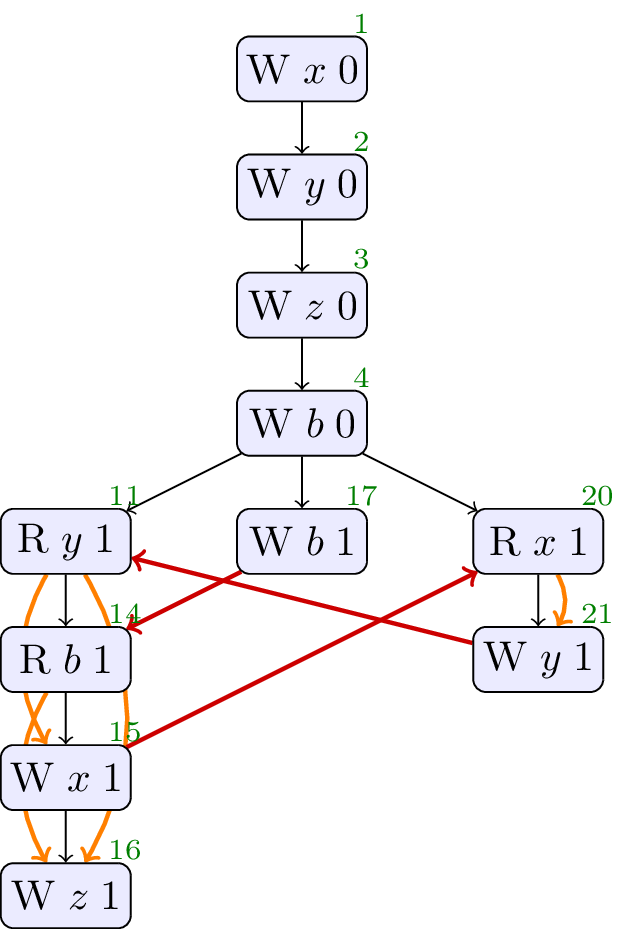
The explanation of why this might be reasonable is rather different to the workings of the C++ concurrency model. It hinges on changing the write that the read on Thread 2 gets its value from, from the else branch on Thread 0 to the true branch. In this pattern of reasoning, we note that the read of b on Thread 0 could read 0 from the initalisation, leading to the else branch and a write of 1 to x. Then Thread 2 can read 1 from x and write 1 to y. Now we reconsider the execution of Thread 0, changing the read of b so that it reads 1 from Thread 1. Correspondingly, we change the control flow of Thread 0 so that it follows the true branch and writes 1 to x and z, allowing the execution above.

We do not have a sequence of optimisations that leads to this behaviour, we believe this execution should be forbidden, and the sdep edges should be as shown above. Does SG1 agree?

3.4. CohCYC

This example also has an execution that is contentious among concurrent models of dependency [WeakestMO]. The program has apparent control dependencies from x to y on Thread 0 and from y to x on Thread 1.

// Init:
x := 0;
y := 0;

// Thread 0:
x := 2;
r1 := x;
if(¬r1 == 2) {
  y := 1
}

// Thread 1:
x := 1;
r2 := x;
r3 := y;
if(¬r3 == 0) {
  x := 3
}

In the execution of concern, Thread 1 reads the value 2 from x, and then follows a typical control-dependent load from y and store to x. The explanation of why this might be reasonable hinges on changing the write that satisfies the condition on Thread 0. Thread 0 will write 1 to y if it reads 1 from x on Thread 1. Then, if we read 1 from y on Thread 1, 3 will be written to x. Now, so the reasoning goes, reading 3 from x on Thread 0 will also satisfy the conditional and lead to the write of y, so we can swap to reading from the write of 3 to x.

We do not have a sequence of optimisations that leads to this behaviour, we believe this execution should be forbidden, and the sdep edges should be as shown above. Does SG1 agree?

3.5. Freeze Example

The most tricky example program and optimisation sequence we have is from Ori Lahav and Chung-Kil Hur.

// Init:
k := 0;
x := 0;
y := 0;
z := 0;
boom := 0;

// Thread 0:
r1 := z;
x := r1

// Thread 1:
r2 := k.load(acq);
if(r2 == 42) {
  r3 := x;
  if(r3 == 1) {
    z := r3;
    boom := 1
  } else {
    r4 := y.load(na);
    z := r4
  }
}

// Thread 2:
y.store(1, na, normal);
k.store(42, rel, normal)

In this test, we could reason that an execution that stores 1 to boom could be allowed. This depends on the sdep edges that we apply in the following execution. Note, we include enough sdep edges here to forbid the behaviour. We will go on to discuss a series of optimisations that may or may not be reasonable. If the optimisation sequence is reasonable, it would lead to removing one of the sdep edges and allowing the behaviour.

The optimisation sequence hinges on the use of a new freeze operation in LLVMIR that allows the compiler to make assumptions about the values read by non-atomics. Use of freeze can produce LLVM poison values, whose values are inteterminate, and can lead to undefined behaviours. We would like the SG1 opinion on the freeze optimisation.

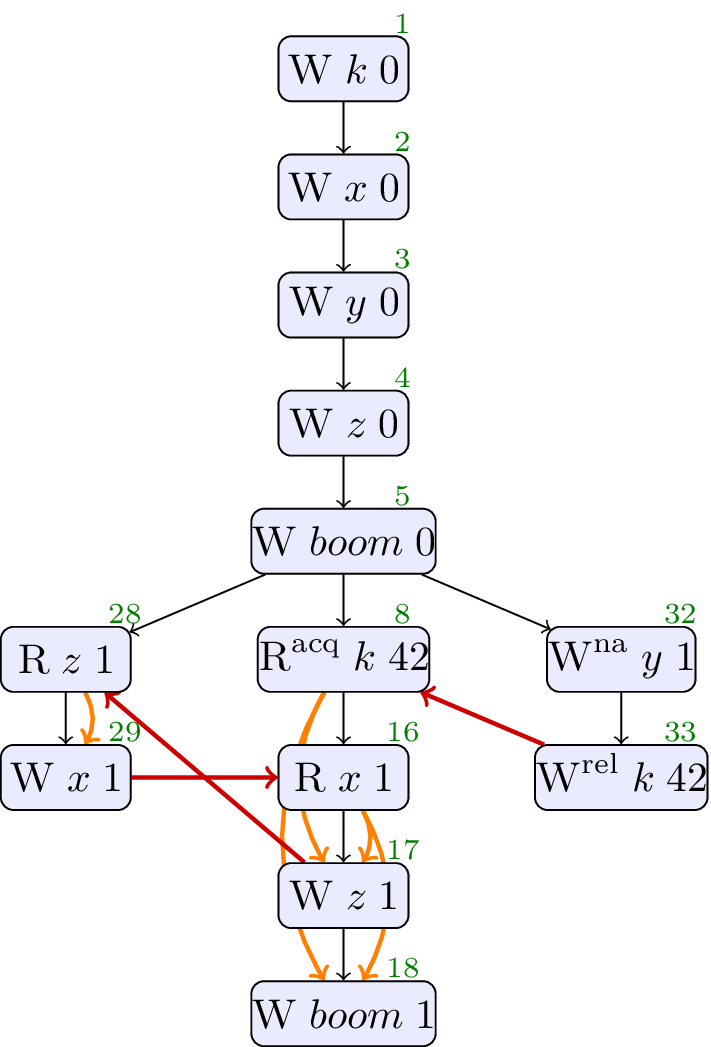
The cycle in sdep and rf that forbids this outcome is over events 16, 17, 28 and 29. The question is whether there should be an sdep edge from event 16 to event 17: from the load of x to the store of z on Thread 1.

The series of optimisations that might remove that sdep edge and permit this behaviour relies on global analysis. The optimisations are all on Thread 1, and we repeat the transformed program after each step. To start with, Thread 1 is as follows.

// Thread 1:
r2 := k.load(acq);
if(r2 == 42) {
  r3 := x;
  if(r3 == 1) {
    z := r3;
    boom := 1
  } else {
    r4 := y.load(na);
    z := r4
  }
}

Load introduction

We introduce a non-atomic load of y into r5. This step relies on global knowledge: introducing a non-atomic in the general case may introduce a race, but here a global analysis could infer that the only other access of y, on Thread 2, is not racy because the if on Thread 1 guards against it, ensuring happens-before if the read is run.

// Thread 1:
r2 := k.load(acq);
if(r2 == 42) {
  r5 := y.load(na);
  r3 := x;
  if(r3 == 1) {
    z := r3;
    boom := 1
  } else {
    r4 := y.load(na);
    z := r4
  }
}

Load forwarding

We replace the non-atomic load of y in the else branch with r5 from our introduced non-atomic load.

// Thread 1:
r2 := k.load(acq);
if(r2 == 42) {
  r5 := y.load(na);
  r3 := x;
  if(r3 == 1) {
    z := r3;
    boom := 1
  } else {
    r4 := r5; // load forward
    z := r4
  }
}

LLVM trace preserving transformation

We freeze the non-atomic load of y at value 1. This adds a branch on freeze(r5==1). In the true case of the branch, the compiler can optimise with the knowledge that r5==1, but in the else branch, r5 carries a poison value that may lead to undefined behaviour.

// Thread 1:
r2 := k.load(acq);
if(r2 == 42) {
  r5 := y.load(na);
  if (freeze(r5==1)) { // freeze
    r3 := x;
    if(r3 == 1) {
      z := r3;
      boom := 1
    } else {
      r4 := r5;
      z := r4
    }
  } else {
    /* ... */
  }
}

LLVM trace preserving transformation

We simplify terms using the predicates on branches.

// Thread 1:
r2 := k.load(acq);
if(r2 == 42) {
  r5 := y.load(na);
  if (freeze(c==1)) {
    r3 := x;
    if(r3 == 1) {
      z := 1; // simplification r3 == 1
      boom := 1
    } else {
      r4 := 1; // simplification using freeze(r5==1)
      z := r4
    }
  } else {
    /* ... */
  }
}

LLVM trace preserving transformation

Here we constant propagate the register value into the store on z and then hoist the z := 1 out of the conditional. The else branch is now empty.

// Thread 1:
r2 := k.load(acq);
if(r2 == 42) {
  r5 := y.load(na);
  if (freeze(c==1)) {
    r3 := x;
    z := 1; // hoisted
    if(r3 == 1) {
      boom := 1
    }
    else { }
  } else {
    /* ... */
  }
}

There is now no dependency between r3 := x and z := 1 so they can be hardware re-ordered. In context with the rest of the program r3 == 1 is now observable and the program can store 1 to boom. This execution would be allowed if the sdep edge were removed between events 16 and 17 in the execution above.

Note that this execution is race-free, the non-atomic store is happens-before the load, thanks to the release/acquire pair on k.

Is SG1 happy with this set of transformations? Should this weak execution be allowed?

4. sdep in Java Causality Tests

To contextualise sdep with the Java Causality Tests, we print the tests, the interesting execution, and our conclusion on acyclicity of sdep and rf. See [JCT].

4.1. JCTC1

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
if(r1 >= 0) {
  y := 1
}

// Thread 1:
r2 := y;
x := r2

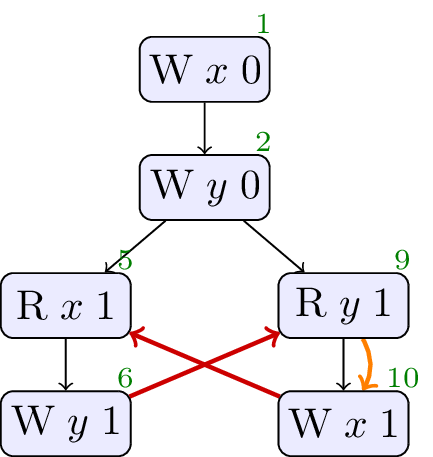
Allowed, no cycle. A compiler can observe that x is always greater than or equal to zero.

4.2. JCTC2

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
r2 := x;
if(r1 == r2) {
  y := 1
}

// Thread 1:
r3 := y;
x := r3

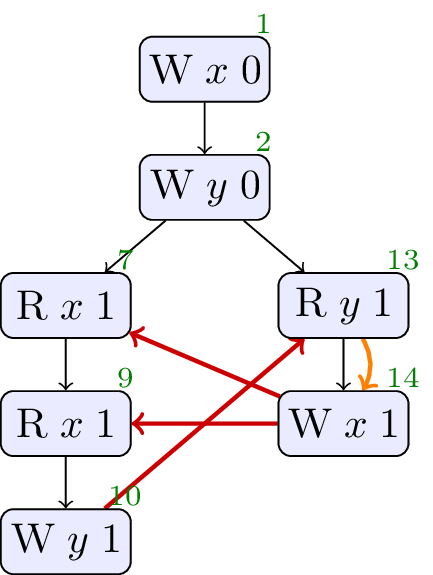
Allowed, no cycle. A compiler can assert that two relaxed loads to the same location will yield the same value.

4.3. JCTC3

// Init:
x := 0;
y := 0;

// Thread 0:
x := 2

// Thread 1:
r1 := x;
r2 := x;
if(r1 == r2) {
  y := 1
}

// Thread 2:
r3 := y;
x := r3

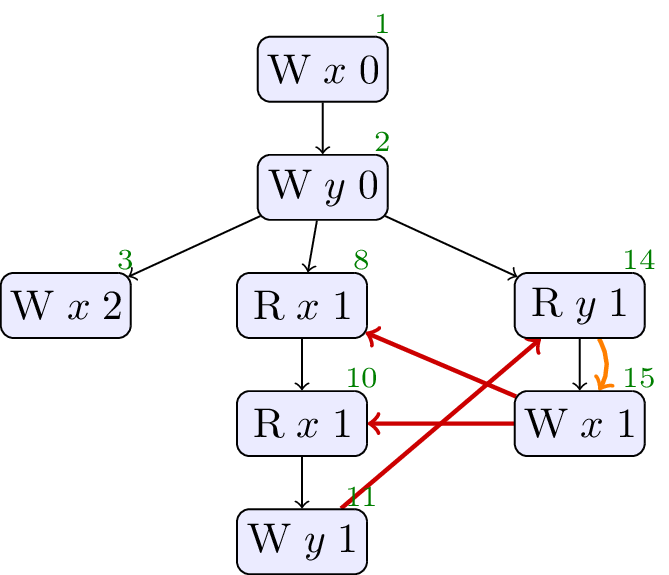
Allowed, no cycle. Similar to above.

4.4. JCTC4

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
y := r1

// Thread 1:
r2 := y;
x := r2

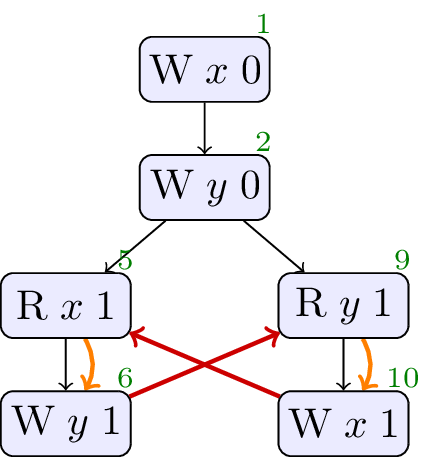
Forbidden, cycle in sdep ∪ rf. No values from thin air.

4.5. JCTC5

// Init:
x := 0;
y := 0;
z := 0;

// Thread 0:
z := 1

// Thread 1:
r3 := z;
x := r3

// Thread 2:
r2 := y;
x := r2

// Thread 3:
r1 := x;
y := r1

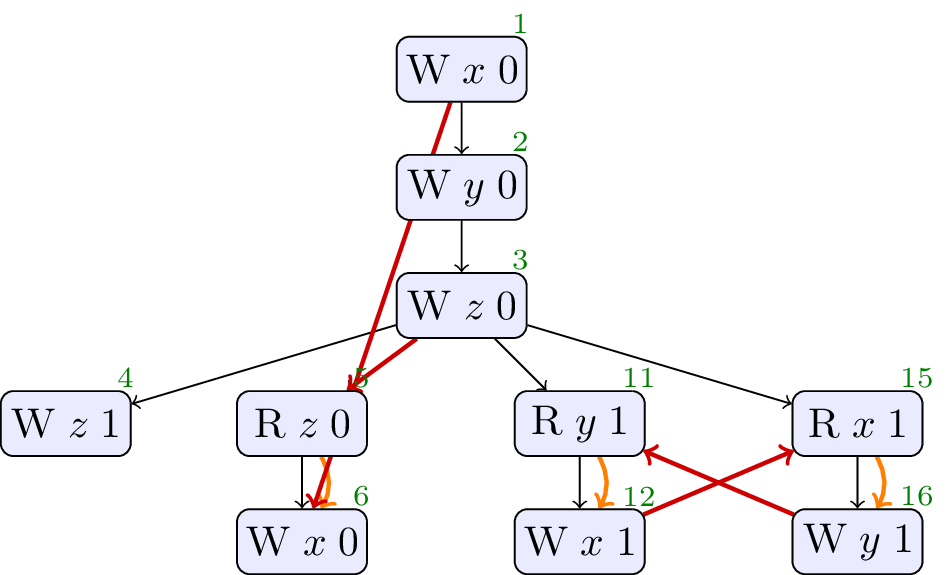
Forbidden, cycle in sdep ∪ rf. No values from thin air.

4.6. JCTC6

// Init:
A := 0;
B := 0;

// Thread 0:
r1 := A;
if(r1 == 1) {
  B := 1
}

// Thread 1:
r2 := B;
if(r2 == 1) {
  A := 1
};
if(r2 == 0) {
  A := 1
}

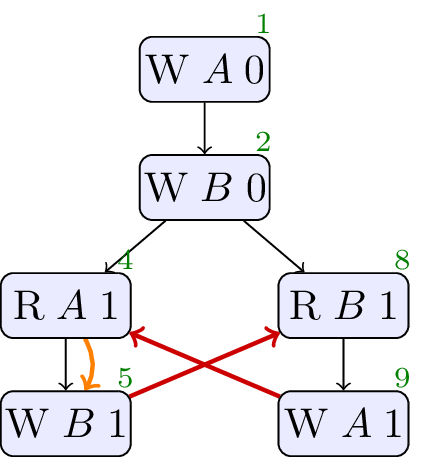
Allowed, no cycle. A compiler can observe that the if cases cover all possible values of B in this program, so there is always a store of 1 to A.

4.7. JCTC7

// Init:
x := 0;
y := 0;
z := 0;

// Thread 0:
r1 := z;
r2 := x;
y := r2

// Thread 1:
r3 := y;
z := r3;
x := 1

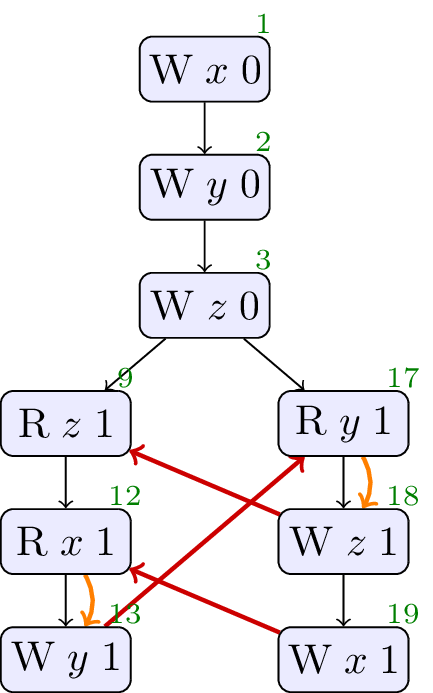
Allowed, no cycle. Hardware and compiler reordering makes this observable.

4.8. JCTC8

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
r2 := (1 + (r1 * r1 - r1));
y := r2

// Thread 1:
r3 := y;
x := r3

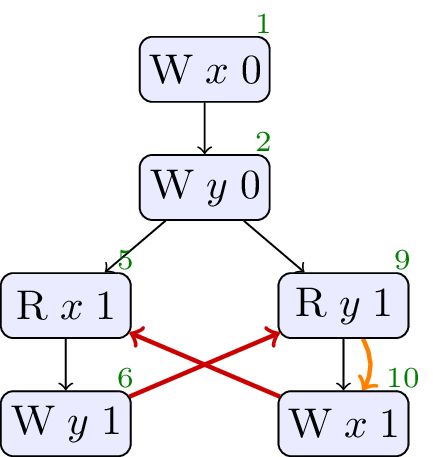
Allowed, no cycle.

Interthread analysis could determine that x and y are always either 0 or 1, and thus determine that r2 is always 1. Once this determination is made, the write of 1 to y could be moved early in thread 1.

4.9. JCTC9

// Init:
x := 0;
y := 0;

// Thread 0:
x := 2

// Thread 1:
r1 := x;
y := (1 + (r1 * r1 - r1))

// Thread 2:
r3 := y;
x := r3

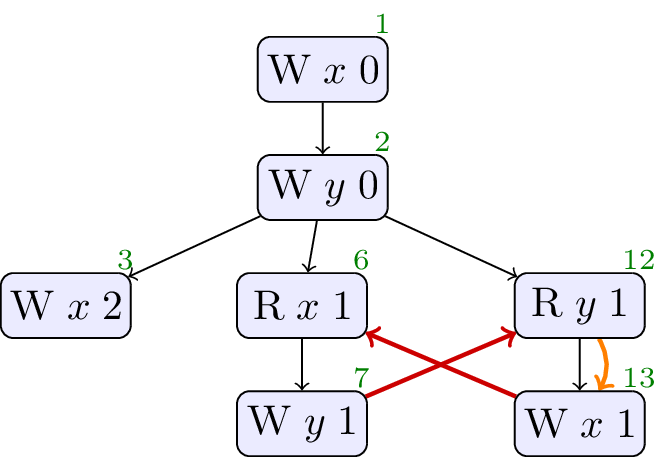
Allowed, no cycle.

Allowed. Similar to test case 8, except that the x is not always 0 or 1. However, a compiler might determine that the read of x by thread 2 will never see the write by thread 3 (perhaps because thread 3 will be scheduled after thread 1). Thus, the compiler can determine that r1 will always be 0 or 1.

4.10. JCTC10

// Init:
x := 0;
y := 0;
z := 0;

// Thread 0:
r3 := z;
if(r3 == 1) {
  x := 1
}

// Thread 1:
r2 := y;
if(r2 == 1) {
  x := 1
}

// Thread 2:
z := 1

// Thread 3:
r1 := x;
if(r1 == 1) {
  y := 1
}

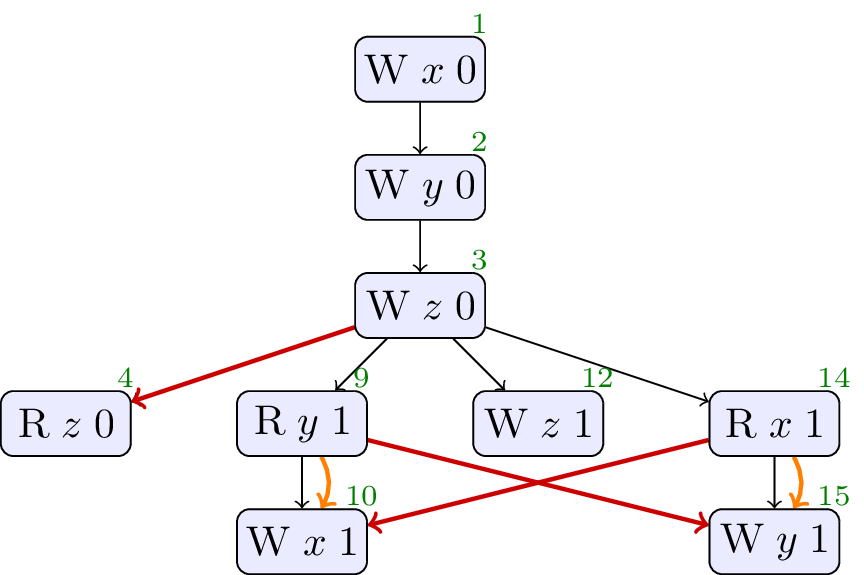
Forbidden, cycle in sdep ∪ rf. No values from thin air.

4.11. JCTC11

// Init:
w := 0;
x := 0;
y := 0;
z := 0;

// Thread 0:
r1 := z;
w := r1;
r2 := x;
y := r2

// Thread 1:
r4 := w;
r3 := y;
z := r3;
x := 1

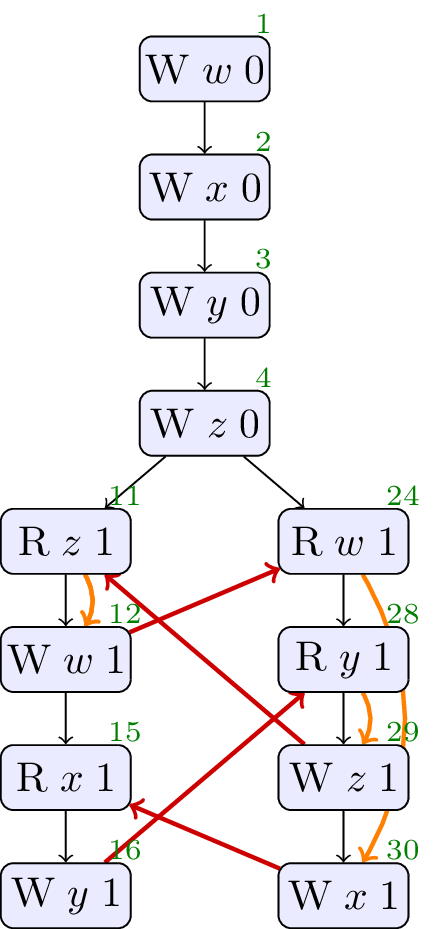
Allowed, no cycle. Observable through compiler and hardare re-ordering.

4.12. JCTC12

// Init:
x := 0;
y := 0;
a0 := 1;
a1 := 2;

// Thread 0:
r1 := x;
if(r1 == 0) {
  a0 := 0
}
else
{
  if(r1 == 1) {
    a1 := 0
  }
};
r2 := a0;
y := r2

// Thread 1:
r3 := y;
x := r3

Forbidden, cycle in sdep ∪ rf. No values from thin air.

4.13. JCTC13

// Init:
x := 0;
y := 0;

// Thread 0:
r1 := x;
if(r1 == 1) {
  y := 1
}

// Thread 1:
r2 := y;
if(r2 == 1) {
  x := 1
}

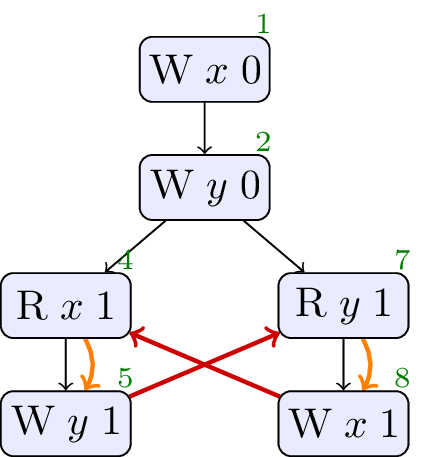
Forbidden, cycle in sdep ∪ rf. No values from thin air.

4.14. JCTC14

We skip this as it involves loops.

4.15. JCTC15

We skip this as the test probes Java’s weak coherence-order guarantees, and is not relevant to C++.

4.16. JCTC16

We skip this as the test probes Java’s weak coherence-order guarantees, and is not relevant to C++.

4.17. JCTC17

We skip this as the test probes Java’s weak coherence-order guarantees, and is not relevant to C++.

4.18. JCTC18

See § 2.6 Java Causality Test Case 18.

4.19. JCTC19

We skip this as it probes thread joining, which is out-of-scope for this paper.

4.20. JCTC20

We skip this as it probes thread joining, which is out-of-scope for this paper.